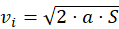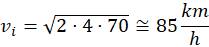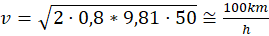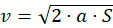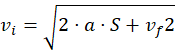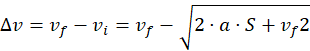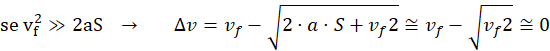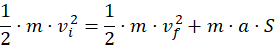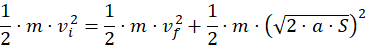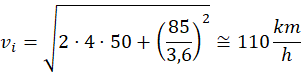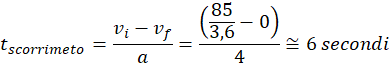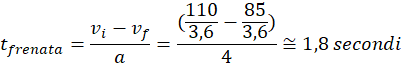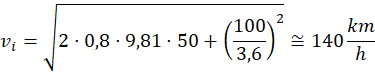Durante il nostro lavoro di ricostruttori ci sono formule e procedure che affrontiamo in modo ricorrente e che applichiamo nella maggior parte dei casi che trattiamo. Questo agire abitudinario può però rivelarsi pericoloso, perché piano piano la formula crea nella nostra mente un concetto assoluto, che smettiamo di analizzare con spirito critico.
Una notevole insidia riguarda la formula più usata nell'attività del ricostruttore:
cioè la formula che data una distanza di frenata (o in generale di rallentamento) ci fornisce la velocità all'inizio della frenata (*).
Questa formula banale, data per scontata, può portare ad errori concettuali molto gravi.
Prendiamo l'esempio di un motociclo che cade al suolo e, scorrendo, percorre una distanza di circa 70 metri. Utilizzando la formula di cui sopra ci faremmo subito un'idea della velocità del motociclo al momento della caduta. Ad esempio (con a=4m/s^2):
Sempre nel nostro esempio, sappiamo che il motociclo prima di cadere ha frenato non in bloccaggio per circa 50 metri.
A questo punto, siamo portati a pensare: "la decelerazione in frenata, non in bloccaggio, potrebbe essere simile a quella di scorrimento e la distanza di frenata è poco inferiore a quella di scorrimento. Quindi in frenata la moto avrà rallentato poco meno di quanto ha fatto scorrendo... Magari sui 50 metri di frenata avrà rallentato di 60-70 km/h, al posto degli 85km/h che ha perso sui 70 metri scorrendo".
Un ulteriore esempio può essere quello di un tamponamento in autostrada. Supponiamo di essere sicuri che il tamponante al momento dell'urto procedesse a 100 km/h e che, prima dell'urto, abbia lasciato ben 50 metri di frenata in bloccaggio… "Se all'urto facevo 100 all'ora, chissà a quanto andava prima, con 50 metri di frenata!" questo è sicuramente il primo pensiero che ci verrebbe in mente. E il secondo pensiero sarebbe: "Con 50 metri di frenata la velocità persa è solo per la frenata è:
In più è arrivato all'urto a 100 all'ora, questo andava come un pazzo."
Il problema dei ragionamenti portati negli esempi è proprio l'uso abituale della formula
che costruisce nella nostra mente il concetto: "nota la distanza percorsa in frenata si deduce direttamente la velocità". Questo assunto è sbagliato ma è talmente abitudinario che quando prima ho scritto: "(…) la formula che data una distanza di frenata (o in generale di rallentamento) ci fornisce la velocità all'inizio della frenata (…)", ti sarà sembrata una frase assolutamente normale. Ma in realtà la frase è errata, seppure faccia parte del dire quotidiano. La frase corretta è:
Vediamo perché.
La formula estesa, da cui discende quella semplificata che usiamo tutti i giorni, è la seguente:
Questa formula ci dice che la velocità all'inizio di una frenata non dipende solo dalla distanza percorsa ma anche dalla velocità alla fine della decelerazione. Soltanto che nell'uso quotidiano ci riferiamo quasi sempre al caso particolare di velocità finale nulla (vf=0) e, piano piano, ci dimentichiamo che " vf" esiste.
Ma "vf" esiste ed influisce notevolmente sul valore della velocità persa in frenata, cioè sul valore del Δv associato alla frenata, pari a:
Dalla formula vediamo che il rallentamento, per una certa frenata di lunghezza "S", è molto influenzato dalla velocità finale. Ancora più precisamente, data una frenata di lunghezza "S", il Δv è tanto minore quanto è più alta la velocità alla fine della frenata. Addirittura, se la velocità finale è molto alta, così la velocità finale al quadrato sia molto maggiore di "2aS", il rallentamento in frenata diventa trascurabile.
Ma quale è la spiegazione di questo fenomeno?
In realtà è molto semplice e possiamo darla in due modi.
Come prima dimostrazione, dobbiamo pensare che il cambio di velocità subito da un veicolo in frenata, dipende dalla decelerazione moltiplicata il tempo di frenata:
Pertanto, data una certa distanza di frenata, tanto più alta è la velocità iniziale del veicolo tanto minore è il tempo impiegato per percorrere la distanza, e quindi minore è il rallentamento.
Per fare un esempio:
- un veicolo che frena in bloccaggio (a=7,85m/s2) per 10 metri, partendo da 100 km/h, impiega meno di 0,4 secondi per percorre i 10 metri, e al termine della frenata la sua velocità è pari a 89 km/h, con un rallentamento di soli 11 km/h,
- un veicolo che frena in bloccaggio (a=7,85m/s2) per 10 metri, partendo da 45 km/h, impiega 1,6 secondi per percorrere i 10 metri, e al termine della frenata è praticamente fermo, con un rallentamento di ben 45 km/h.
Perché questa notevole differenza di rallentamento, anche se i veicoli frenano con la stessa intensità e per la stessa distanza? Proprio perché il secondo veicolo impiega un tempo quadruplo a percorre i 10 metri (da cui il rallentamento 4 volte maggiore).
Come seconda dimostrazione, possiamo passare dalla conservazione dell'energia, la quale ci dice che:
Cioè:
Vediamo quindi che, concettualmente √(2aS), può essere vista come una "velocità" che rappresenta l'energia persa in frenata. Ma tanto più l'energia cinetica alla fine della frenata ( 1/2mvf^2) è elevata, tanto più l'energia persa in frenata diventa trascurabile.
Per concludere, tornando ai nostri esempi, nel caso del motociclo, all'inizio della frenata la sua velocità può essere calcolata con:
E quindi durante la frenata, la moto ha rallentato di: 110-85=25km/h, ben inferiori ai 60-70 km/h di rallentamento che avremmo ipotizzato dal ragionamento abitudinario (errato).
Come prova del 9, possiamo anche calcolare il tempo richiesto al motociclo per percorrere i 70 metri in scorrimento e i 50 metri in frenata:
Come attesto, il tempo di frenata è circa 1/3 di quello di scorrimento, da cui il cambio di velocità durante la frenata è tre volte minore.
Lo stesso vale per l'esempio del tamponamento in autostrada, per cui la velocità dell'autoveicolo all'inizio della frenata è:
Cioè durante i 50 metri di frenata il veicolo ha rallentato di 140-100=40km/h, rispetto ai 100km/h che avevamo ricavato dall'errato ragionamento abitudinario.