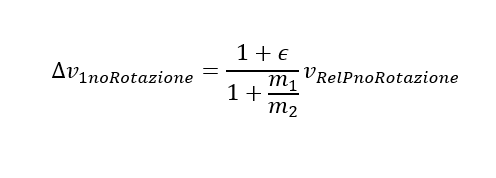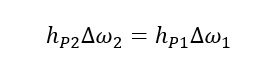Nel vasto mondo di internet si trovano le più disparate formule, alcune dal sapore magico, per collegare il Δv dei veicoli alla velocità relativa all'urto e alla PDOF, ma nella maggior parte dei casi tutte queste relazioni servono solo a confondere le idee. In questo articolo un piccolo riassunto per fare chiarezza.
L'origine di tutta la confusione risiede nell'insensata ricerca di formule "furbe" per ricavare senza sforzo quello che invece si potrebbe ottenere molto prima con un po' di ragionamento. Per i veicoli in collisione, questo ragionamento risiede nella ricostruzione dell'urto fra autoveicoli con un modello di collisione impulsivo.
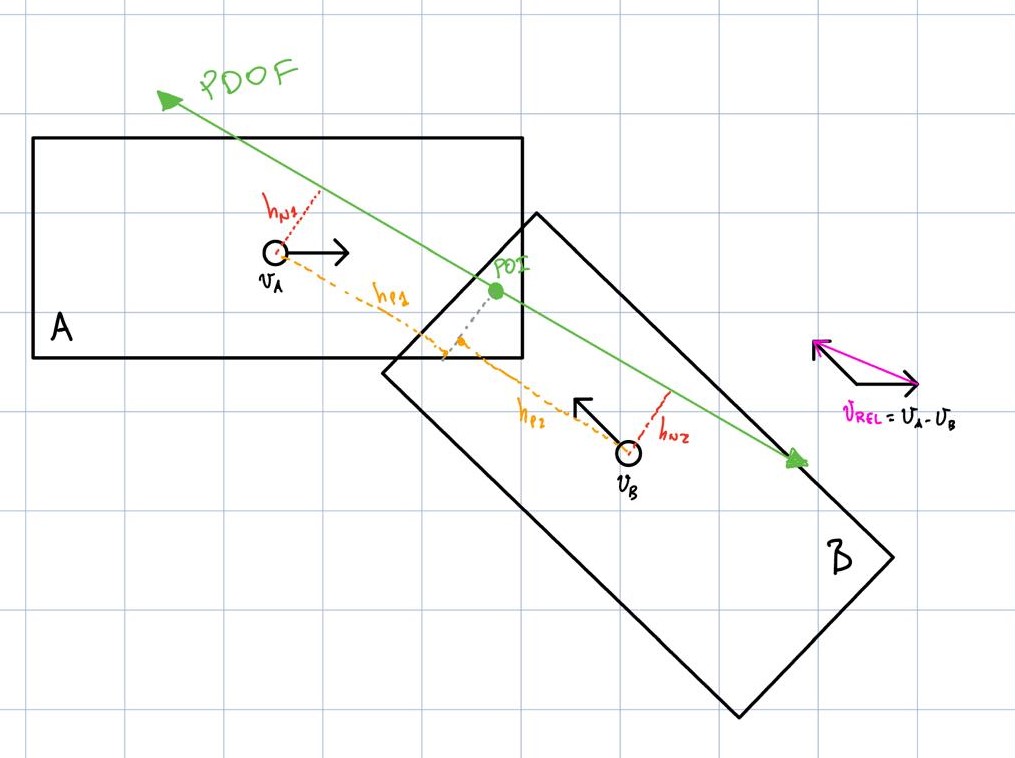
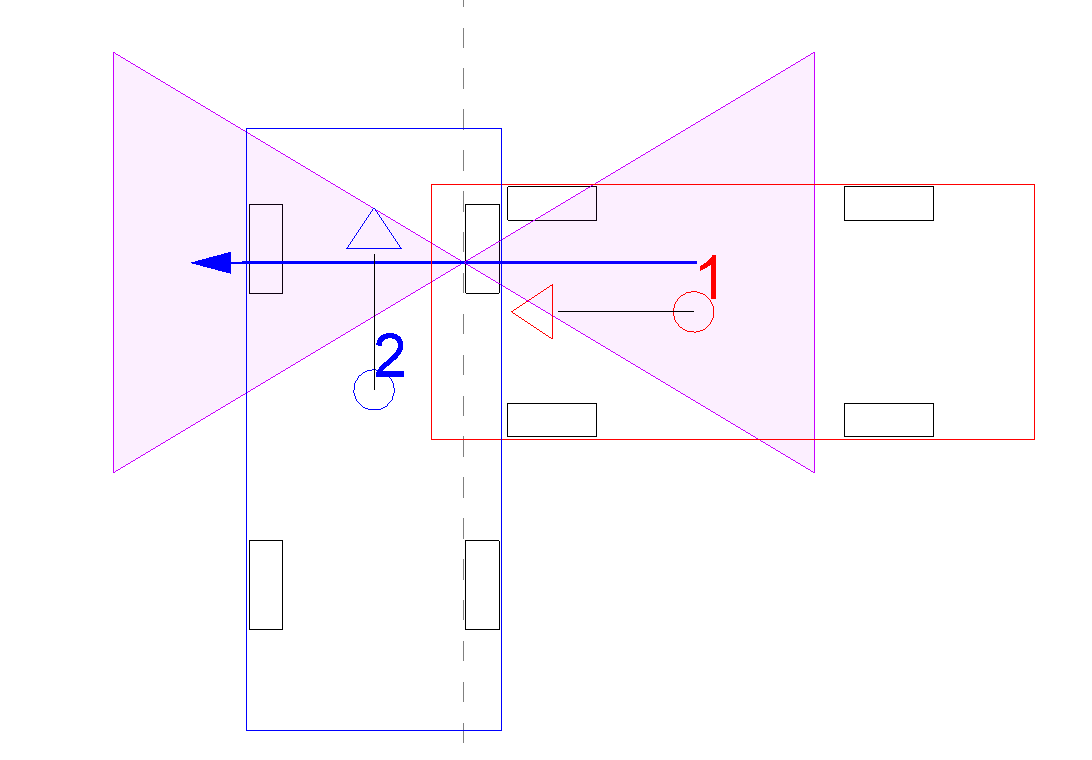
Non daremo la dimostrazione, ma applicando a un sistema di due veicoli (vedi immagine) la prima e la seconda equazione cardinale, rispetto a un sistema di riferimento in cui:
- l'asse x coincide con la PDOF (rispetto al veicolo 1);
- l'asse y è definito secondo la terna levogira;
si ottengono le seguenti relazioni, che legano i Δv dei veicoli alla velocità relativa all'urto:
Dove:
- vRelP è la velocità relativa all'urto dei veicoli lungo la direzione della PDOF (rispetto al veicolo 1)
- vRelN è la velocità relativa all'urto dei veicoli lungo la direzione ortogonale alla PDOF (rispetto al veicolo 1)
- Δv è il cambio di velocità sperimentato dai veicoli per l'urto
- Δω è il cambio di velocità angolare di imbardata sperimentato dai veicoli per l'urto
- hN è il braccio dell'impulso in direzione normale alla PDOF (cioè la distanza fra il centro di massa del veicolo e la retta di applicazione dell'impulso)
- k è il raggio giratore (che identifica il momento di inerzia del veicolo)
- hP è il braccio dell'impulso in direzione parallela alla PDOF
- ϵ è il coefficiente di restituzione
Queste tre equazioni sono tutto quello di cui si ha bisogno e, osservate, rivelano dettagli interessanti sulla dinamica di una collisione:
- dalla (3):
- come noto, nel caso in cui non ci siano bracci (hN=0) non c'è rotazione; cioè se la PDOF passa per il centro di massa di un veicolo questo non sperimenta rotazione;
- dalla (1):
- come lecito aspettarsi, il contributo dei Δv rileva solo per la velocità relativa in direzione della PDOF, dato che il Δv ha la stessa direzione dell'impulso, cioè la PDOF è anche la direzione del Δv;
- nel caso in cui ci siano rotazioni, la velocità relativa viene distribuita tra i Δv e tra i Δω;
- dalla (2):
- se non ci sono rotazioni la PDOF ha sempre la direzione della velocità relativa (perché vRelN = 0); solo in caso di rotazioni la PDOF può avere una direzione diversa dalla velocità relativa.
IMPLICAZIONI
Le considerazioni precedenti comportano le seguenti implicazioni:
Nel caso di urto in cui la PDOF passa per il centro di massa, i veicoli non subiranno rotazioni, il Δv avrà la stessa direzione della velocità relativa pre-urto e, in modulo, sarà maggiore rispetto tutte le altre possibili configurazioni in cui i veicoli (a parità di velocità relativa) subiscono, rotazioni. In questo caso infatti, dalla (1) e tenendo conto che Δv1/Δv2=m2/m1:
Nella formula il pedice: "noRotazione" serve per indicare che in questo esempio non ci sono rotazioni.
A parità di velocità relativa all'urto, se i veicoli sperimentano rotazioni, i Δv saranno più bassi del caso in cui non ci siano rotazioni, perché una quota della velocità relativa verrà "trasformata" in rotazione post-urto, come emerge dall'equazione (2) di sopra. Inoltre, a seconda della configurazione d'urto, dalla (3) può sussistere anche una componente normale alla PDOF per la velocità relativa. Letto in altro modo, questo significa che la PDOF non ha più (come nel caso precedente) la stessa direzione della velocità relativa e quindi in questo caso, la velocità relativa in direzione della PDOF è vrelPconRotazione < vRelPnoRotazione (come era prima).
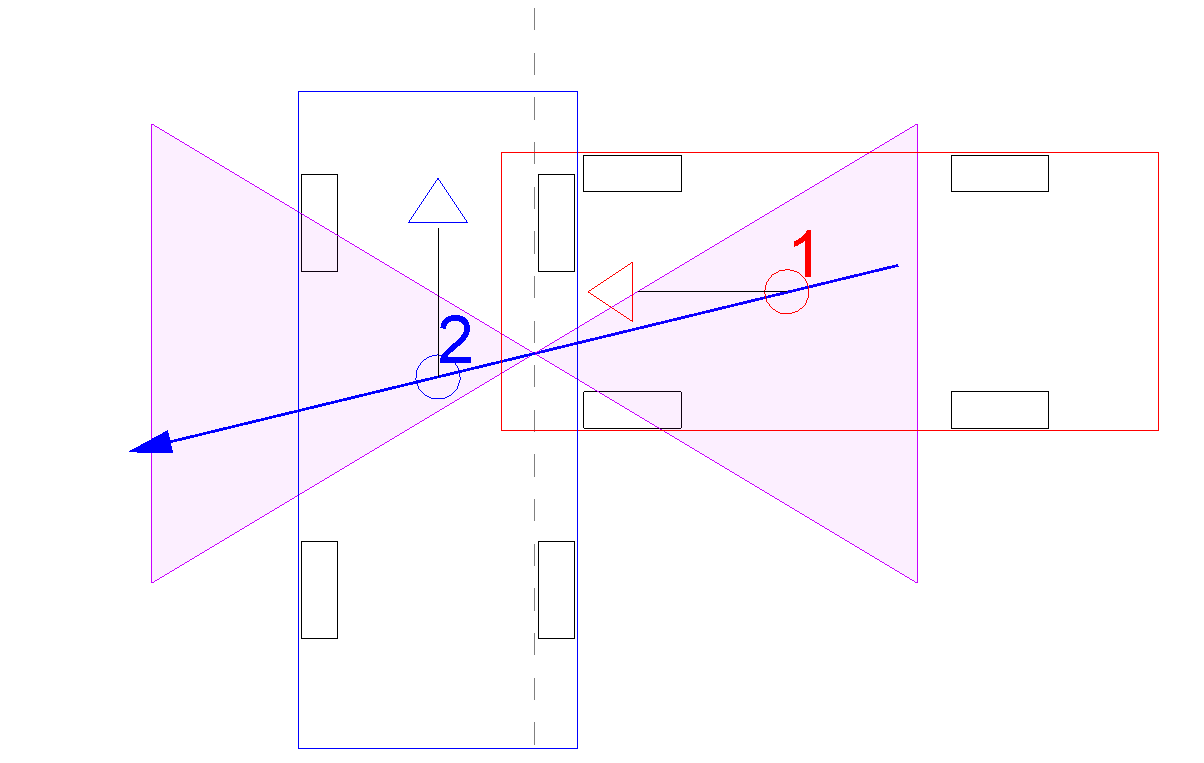
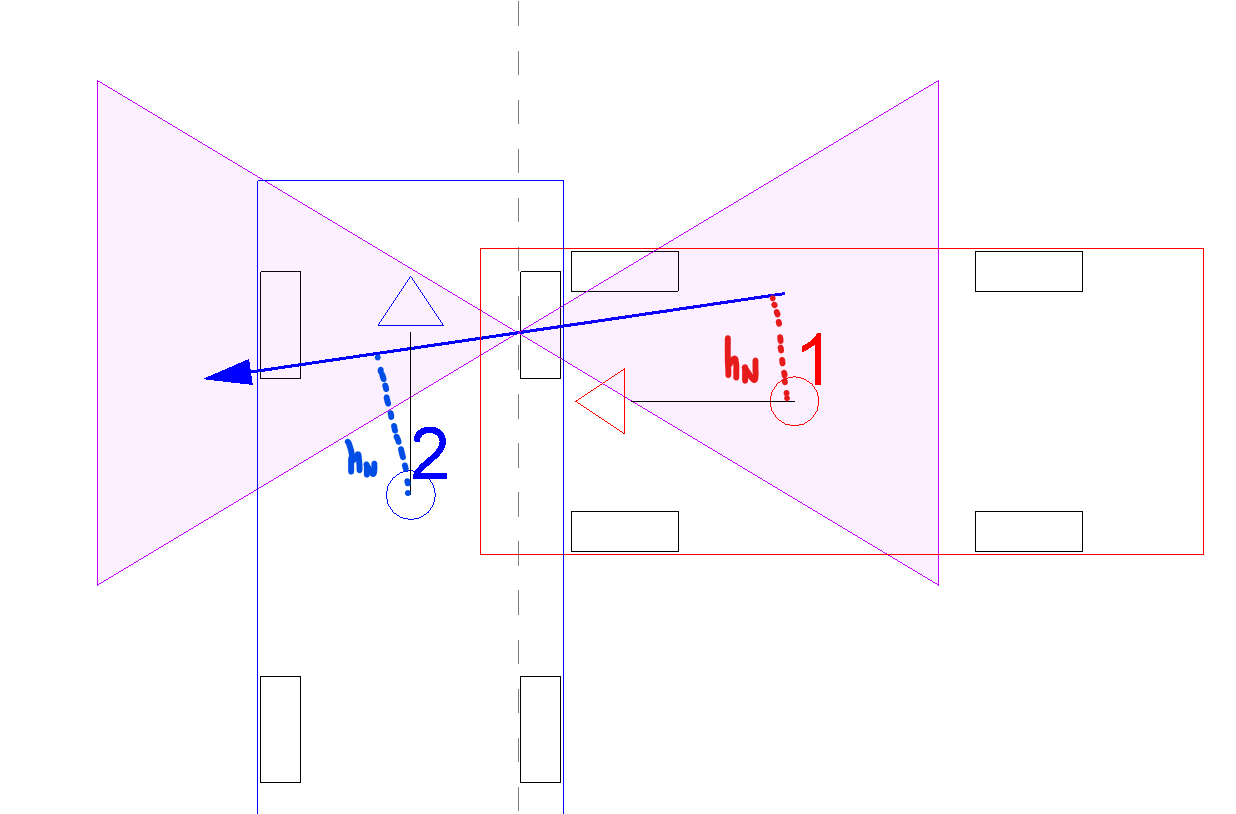
Non necessariamente la presenza di rotazioni significa che la velocità relativa ha sempre una componente ortogonale alla PDOF, cioè non sempre la PDOF e la velocità relativa hanno direzioni diverse nel caso di rotazioni. Dalla (2), vediamo che nel caso particolare in cui:
la velocità relativa in direzione normale alla PDOF è nulla, e quindi la PDOF ha la stessa direzione della velocità relativa, come nell'esempio a fianco.